3D Map Objects part 1

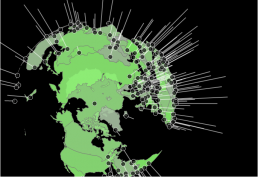
I am sure many of you Qlikkers out there have tried to use the Qlik Sense native map object to visualise data for cities, regions, countries, and continents, and perhaps some of you also have used the map object to visualise polygons for floor plans or details in various objects. Visualising map data is a simple process. I will not go into details on how that is done in this blog as there are plenty of guidelines for that online. Instead, I will explain how to project your 2-dimensional map to a 3D Sphere! And all it takes is 2 lines of code!

Sounds interesting?

I’m keeping this blog first post as simple as I can. I will not explain how the math works. I will focus only on how to apply the maths on your map object.

But first, just some very basics things you should know:

Cartesian coordinate system.

You probably already know what a Cartesian Coordinate System is, even if you feel unsure because you might have forgotten the name of it. In simple words; a 2 dimensional cartesian coordinate system is a an area / system that has a x axis and a y axis.

Map Object

The map object in Qlik sense is basically a 2-dimensional Cartesian Coordinate System, or perhaps could be described as a “Cartesian Canvas”. It is in my opinion the coolest of all objects because it has so many possibilities! With this object you can plot anything you like – pixels or “Points”, draw straight lines, plot out simple and complex polygons and paint “heat areas”.

The location of dots in the map object is either described in something that is called “location” or as longitude and latitude. A Location field is just a combination of longitude and latitude in this format [Longitude,Latitude]. Think of longitude as x (horizontal axis) and latitude as y (vertical axis). With this, the location field is [x,y]. This describes a 2-dimensional area.

Function Variables

The last thing you need to know is what is a function variable in Qlik Sense.

Here is an example on how to create a function variable that takes two input values and calulates something:

Set vMyFunctionVariable = ‘$1 + sqr ($2)’

And here is how to use the variable:

Let mySumofTwo = $(vMyFunctionVariable(3,2))

In this case, the variable mySumofTwo = 3 + sqr(2) = 3 + 4 = 7

I find those function variables super useful – as they can be used over and over again in your code, including in your application expressions, as you will see in this blog post.

The hidden information in Longitude and Latitude!

When we look at the concept of longitude and latitude for maps of the earth – they are a “flattened projection” of what in reality a 3D sphere (let us assume the Earth is a perfect sphere… keep things simple!).

A sphere is a 3-dimensional object, so it is existing in a 3-dimensional cartesian system – with axis x, y and z.

To project something 3 dimensional to a 2-dimensional area, like we do with when plotting a flat map of the Earth we are using quite basic math formulas like sinus and cosinus, where we need to know the radius of the earth as an important parameter.

Luckily when using math, we can often “reverse” it! So, there is a mathematical way to do the opposite! To “re-project” a flat map of earth back to a sphere.

Hidden in the two dimensions called longitude and latitude we have three dimensions (x, y, z) – it is only a matter of knowing how to convert them back to 3 dimensions and then to understand how to plot those 3 dimensions back into a new 2 dimensional screen but do that in a way so it still “looks 3 dimensional”.

The two rows you need

Here is the 2 magical formulas you need:

Set ReCalcLat = 'EYE_X + SCREEN_DEPTH*tan(atan((($(EARTH_RADIUS) * cos($1*Pi()/180)*cos($2*Pi()/180))-EYE_X) / (($(EARTH_RADIUS) * sin($1*Pi()/180))+SCREEN_DEPTH)))';

Set ReCalcLong= 'EYE_Y + SCREEN_DEPTH*tan(atan((($(EARTH_RADIUS) * cos($1*Pi()/180)*sin($2*Pi()/180))-EYE_Y) / (($(EARTH_RADIUS) * sin($1*Pi()/180))+SCREEN_DEPTH)))';

As you see the formulas require some predefined “constants” : EARTH_RADIUS, SCREEN_DEPTH, EYE_X and EYE_Y. These are variables to describe how your new 3D sphere should be projected on the 2-dimensional map object. To keep things simple, I recommend the following vales as default:

Let EARTH_RADIUS=6378.137; //Earth radius in km.

Let SCREEN_DEPTH = EARTH_RADIUS*2; // DISTANE FROM THE EYE TO THE SCREEN

Let EYE_X = 0; //POSITION OF THE EYE ON THE X-AXIS

Let EYE_Y = 0; //POSITION OF THE EYE ON THE Y-AXIS

And here is how to use the variables (anywhere you want):

Newlat = $(ReCalcLat(latitude,longitude))

Newlong = $(ReCalcLong(latitude,longitude))

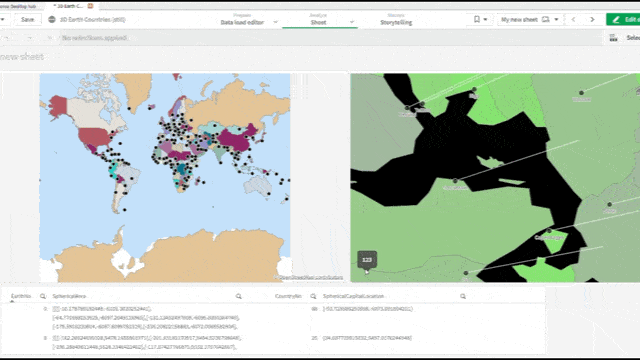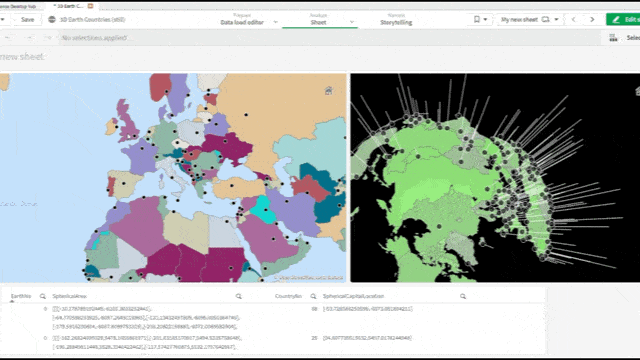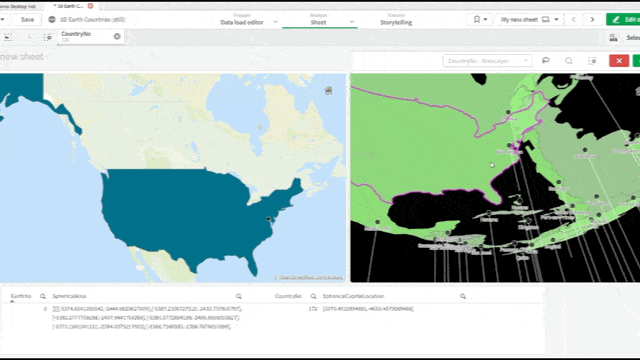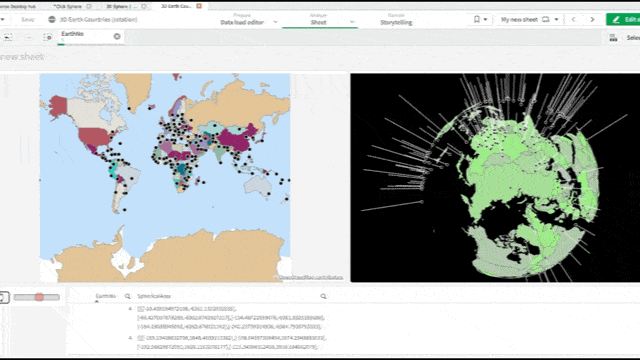
Let us Fly over the earth!

Follow these instructions:

1. Import map data with longitude and latitude values into a new app
   For instance, you can find nice geo data here)
2. Add the code mentioned above
3. Create a map object.
4. Add a point layer to the map object, select your dimension and use the longitude and latitude fields from your data as location.
5. Look at your map and make sure the data is projected correctly.
6. Remove the background map so that you only have a blank background
7. Change “Projection” to “user defined (meters)”.
8. Go back to your point layer and to the location tab. Change your longitude and latitude fields to this:

• Latitude field :  $(ReCalcLat(latitude,(longitude)))
• Longitude field: $(ReCalcLong(latitude,(longitude)))

Enjoy you new, completely responsive, clickable globe!

Next articles in this series will be about

• Part 2: How to project 3D Lines on the 3D Globe using the Line Layer
• Part 3: How to import Country KML files and project them to the 3D Globe using the Area Layer

Article Resources

Try the app live here.

If you are interested in downloading the example app, you can get it from GIT here:

• Map object go 3d (part 1)